The Threat Detection Fundamental Dilemma

Table of Contents
In my role as a CSIRT Engineer, I raised many concerns and critics about low precision analytics. Now, as a member of the Threat Detection team, I am keenly focused on crafting rules that are both useful and precise, aiming to mitigate unnecessary stress in CSIRT caused by alert fatigue. However, the challenge arises when overly precise rules may inadvertently blind us to real malicious activities. This conundrum, which I term the "Threat Detection Fundamental Dilemma," will be the focal point of this post.
Reviewing Terminology
Before delving into the dilemma, let's establish a shared understanding of some terminology related to alert investigation. Any alert handled by CSIRT can be classified within a confusion matrix, comprising the following categories:
- True Positive (TP): An alert raised for a malicious activity, sparking investigation and satisfaction in CSIRT.
- True Negative (TN): No alert raised, indicating a non-malicious event, causing no concern for CSIRT.
- False Positive (FP): An alert raised for a benign activity, leading to frustration and unnecessary stress in CSIRT, potentially contributing to alert fatigue.
- False Negative (FN): No alert raised for malicious activities, a risky scenario as it indicates exploitation without awareness.
The focus here is on TP and FN, which involve relevant events. Keep these in mind as we proceed. Now, armed with this data, we can calculate two crucial metrics: Precision and Recall.
Maintaining a high level of confidence in CSIRT analysis is paramount. Thus, the alert rationale should remain as simple as possible. Incident Responders must tag alerts as TP or FP after triage and if additional metrics are desired, subcategories like Malware and Phishing for TP, and Anomaly and Internal Testing for FP can be created. However, simplicity (KISS) is key to success based on my experience.
Precision
Precision, representing the ratio of FPs a rule generates, is calculated as follows:
$$ Precision = \frac{TP}{TP + FP} $$
This metric, using data from all raised alerts, aids in identifying analytics that may need fine-tuning (low-fidelity rules). The rationale is simple: lower Precision implies a higher probability of contributing to alert fatigue, requiring closer attention.
Recall
In contrast to Precision, which considers irrelevant events (FP), Recall encompasses all relevant events (TP and FN). As it accounts for undetected malicious events (FN), it is harder to calculate. This data may be sourced from various channels, such as manual reports, Purple Team exercises, Threat Huntings, etc. Once FN per rule is obtained, Recall can be calculated using this formula:
$$ Recall = \frac{TP}{TP + FN} $$
Analyzing the equation, it is evident that higher Recall is favorable, indicating the successful identification of numerous malicious events. Thus, rules with a high Recall rate are desired as they mean the detection of a greater proportion of relevant events.
Navigating by Metrics
Precision and Recall are complementary, each monitoring a distinct aspect of the scenario. As previously mentioned, Precision gauges the stress induced in operations due to FPs, while Recall evaluates the risk arising from the failure to detect malicious activities. Consider the following image, based on this amazing example from Wikipedia.
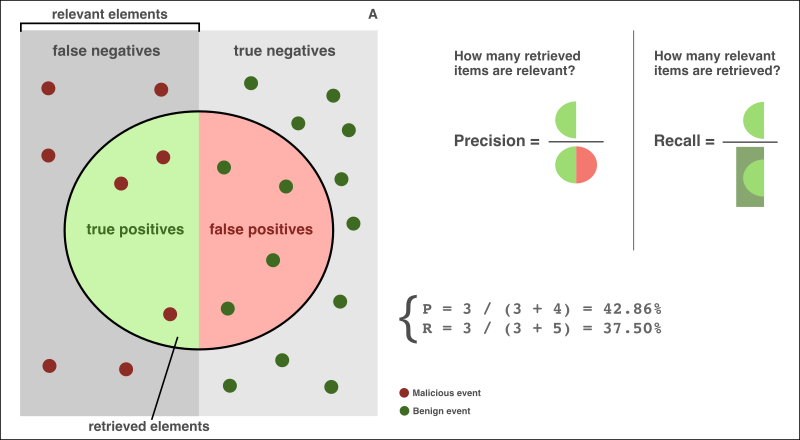
In this image, the FN scope comprises entirely malicious (relevant) events (red dots), whereas the TN scope consists solely of benign events (green dots). The large circle in the center represents the analytic's monitored scope, with every event within it being a detection (alert).
In this example, the Recall ratio is low (37.5%; only 3 out of 8 malicious events were detected), indicating that urgent maintenance for this analytic may be necessary. If the analytic's scope is adjusted to encompass all events in the scenario (benign and malicious), Precision and Recall would be:
$$ P = \frac{8}{8 + 14} = 36.36\% $$
$$ R = \frac{8}{8+0} = 100.00\% $$
This adjustment, while reducing Precision, significantly improves Recall (100% is infeasible, see the next note, but the improvement is evident). Context matters, and in this fictional scenario, it seems like a prudent decision.
As MITRE states, "it is almost impossible to write an analytic that has perfect Precision or perfect Recall, and improving one often comes at the cost of making the other one worse."
The Dilemma Unveiled
Fine-tuning rules appears to be the logical path, doesn't it? As a former CSIRT Engineer, I subscribed to this belief until transitioning to Threat Detection. The crux lies in the fact that our networks typically experience far more benign events than malicious ones, as illustrated in the next image.
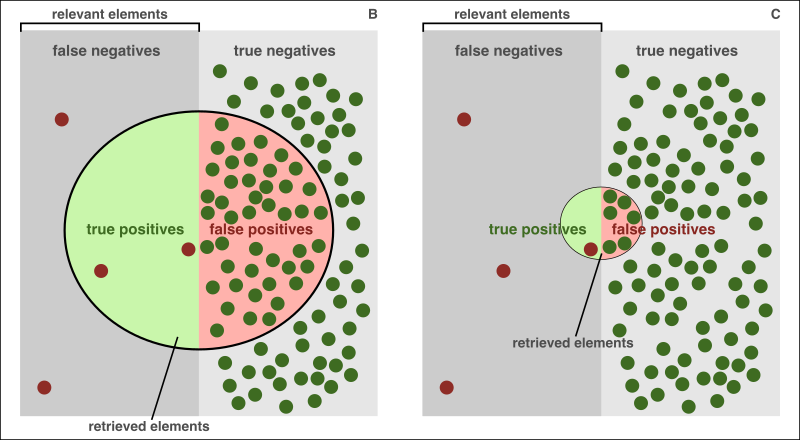
In scenario B (left), Precision is 4.25%, and Recall is 33.33% (calculated below). This scenario is stressful for CSIRT, with 95.75% Noisiness (100% - Precision %). Analytics like this not only contribute to alert fatigue but also foster skepticism among CSIRT Analysts, significantly diminishing the team's awareness.
$$ P = \frac{2}{2 + 45} = 4.25\% $$
$$ R = \frac{2}{2 + 4} = 33.33\% $$
Attempting to fine-tune the rule by applying more filters to narrow down results might lead to scenario C (right). While Precision improves slightly (~10%), alert fatigue is alleviated with 86% fewer detections. However, Recall is reduced (already low), increasing the risk of being compromised without detection -—a less stressful yet dangerous scenario. The calculations are as follows:
$$ P = \frac{1}{1 + 6} = 14.28\% $$
$$ R = \frac{1}{1 + 3} = 25.00\% $$
On the Detection side, there are avenues for improvement. The rule's scope can be altered, changing the events found and leading to a more suitable scenario. Alternatively, a complete shift in approach, such as using different log sources or tools, or adopting a different detection method, can be considered. Quick recap, there are various detection methods:
- Signature-based analytics: Rules describing malicious patterns, commonly used in SIEM or IDS. While offering good Precision, defining and describing patterns is challenging, and deviations may compromise effectiveness. Dependency on previous data renders it quickly outdated.
- Allow-list analytics: Explicitly defining what is allowed and considering everything else as malicious -—the inverse of signature-based. It can introduce friction between security and other teams, reducing productivity, especially in dynamic/innovative environments. Keeping allow-lists up-to-date can be challenging, making them ineffective for large lists, as adversaries may act within the defined standards without deviation.
- Anomaly-based analytics: Assuming statistically "normal" activity is benign and classifying everything else as malicious. Similar to allow-list analytics, but the definition of "normal" is automatic -—compromised environments during the learning phase can render the algorithm ineffective. Despite its capability to detect unknown attacks, it tends to result in low Precision and Recall rates, especially in dynamic environments with constantly changing baselines.
Each approach can be applied to a specific data dimension, as illustrated in the Pyramid of Pain (hash values, IP addresses, domain names, network/host artifacts, tools, and TTPs). If creating effective signature-based analytics proves challenging with network data, switching to anomaly-based analytics within the same dataset or changing the dataset to TTP may be a viable solution.
Note that there is no definitive answer as to whether a specific combination will work. In certain cases, a closed scope may be non-negotiable (demanded by audit, for instance), or after multiple attempts, a satisfactory solution may prove elusive. In such scenarios, finding an acceptable balance between Precision and Recall and implementing compensating controls to address gaps is the best course of action. Voila! This is what I refer to as "The Threat Detection Fundamental Dilemma!"
Key Takeaways
For Threat Detection teams, it is paramount to collect CSIRT analysis for each analytic they're responsible for and calculate Precision and Recall. These metrics aid in prioritizing tasks and identifying low and high-confidence analytics, highlighting strengths and weaknesses.
As there's no perfect software, there's also no perfect analytic, so striving for 0% FP or 100% Recall is unrealistic. This means that achieving a balance between the two is essential for success -—this encapsulates the Threat Detection Dilemma. Employing compensating controls for rules with low Recall is a valid strategy. Creativity becomes our ally.
Several approaches to creating analytics exist, and if one path proves unsuccessful, thinking outside the box and altering it may lead to success. Maintaining the same detection method but changing scopes is a valid consideration, and there are no definitively right or wrong answers. Just remember that after creating an analytic, tracking it throughout its lifecycle against Precision and Recall and periodic updates reflecting changes in the Threat Landscape and our environment are essential.